程序员算法宝典,刷算法使用Java语言,用于编写/存储基本、初级、中级、高级、终极算法处理编码过程。 同时还对其他算法进行原理讲解,例如:paxos、bloomfilter、zab等其他算法。 仓库还在维护过程中,请耐心等待,作者会尽最大努力完成该算法仓库的维护。 若您有问题,或者新的想法,可以提Issues或发送邮件,作者会及时回复您并尽最大努力帮助您 (注:作者目前也是菜鸟,初学阶段。算法收集于知乎、CSDN、百科等。作者只是知识的搬运工,仅部分原创)
排序算法可视化演示可查看 https://visualgo.net/
算法小抄在线阅读: https://labuladong.gitee.io/algo/
github: https://github.com/labuladong/fucking-algorithm
调试运行
节点的左子树小于节点本身
节点的右子树大于节点本身
左右子树同样为二叉搜索树
下图就是一棵典型的二叉搜索树:
二叉搜索树是均衡二叉树的基础,我们看一下它的搜索步骤如何。我们要从二叉树中找到值为 58 的节点。 第一步:首先查找到根节点,值为 60 的节点。
第二步:比较我们要找的值 58 与该节点的大小。 如果等于,那么恭喜,已经找到;如果小于,继续找左子树;如果大于,那么找右子树。 很明显 58<60,因此我们找到左子树的节点 56,此时我们已经定位到了节点 56。
第三步:按照第二步的规则继续找。 58>56 我们需要继续找右子树,定位到了右子树节点 58,恭喜,此时我们已经找到了。
我们经过三步就已经找到了,其实就是我们平时所说的二分查找,这种二叉搜索树好像查找效率很高,但同样它也有缺陷,如下面这样的二叉搜索树。
平衡二叉树是基于二分法的策略提高数据的查找速度的二叉树的数据结构;
平衡二叉树是采用二分法思维把数据按规则组装成一个树形结构的数据,用这个树形结构的数据减少无关数据的检索,大大的提升了数据检索的速度;
平衡二叉树的数据结构组装过程有以下规则:
(1)非叶子节点只能允许最多两个子节点存在。
(2)每一个非叶子节点数据分布规则为左边的子节点小当前节点的值,右边的子节点大于当前节点的值(这里值是基于自己的算法规则而定的,比如hash值);
平衡树的层级结构:因为平衡二叉树查询性能和树的层级(h高度)成反比,h值越小查询越快、为了保证树的结构左右两端数据大致平衡降低二叉树的查询难度一般 会采用一种算法机制实现节点数据结构的平衡,实现了这种算法的有比如TreeMap、红黑树,使用平衡二叉树能保证数据的左右两边的节点层级相差不会大于1, 通过这样避免树形结构由于删除增加变成线性链表影响查询效率,保证数据平衡的情况下查找数据的速度近于二分法查找;
(1)非叶子节点最多拥有两个子节点;
(2)非叶子节值大于左边子节点、小于右边子节点;
(3)树的左右两边的层级数相差不会大于1;
(4)没有值相等重复的节点;
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构;
(1)排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则;
(2)子节点数:非叶节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M阶代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉);
(3)关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2);
(4)特别注意这一点:所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子;
最后我们用一个图和一个实际的例子来理解B树(这里为了理解方便我就直接用实际字母的大小来排列C>B>A)
B树的查询流程:
如上图我要从上图中找到E字母,查找流程如下
(1)获取根节点的关键字进行比较,当前根节点关键字为M,E<M(26个字母顺序),所以往找到指向左边的子节点(二分法规则,左小右大,左边放小于当前节点值的子节点、右边放大于当前节点值的子节点);
(2)拿到关键字D和G,D<E<G 所以直接找到D和G中间的节点;
(3)拿到E和F,因为E=E 所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null);
B树的插入节点流程
定义一个5阶树(平衡5路查找树),现在我们要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来;
遵循规则:
(1)节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分);
(2)排序规则:满足节点本身比左边节点大,比右边节点小的排序规则;
B树节点的删除
(1)节点合并规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须大于等于ceil(5/2)(这里关键字数<2就要进行节点合并);
(2)满足节点本身比左边节点大,比右边节点小的排序规则;
(3)关键字数小于二时先从子节点取,子节点没有符合条件时就向向父节点取,取中间值往父节点放;
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库中的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的, 每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘快大小范围; 把树的节点关键字增多后树的层级比原来的二叉树少了,减少数据查找的次数和复杂度;
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;
(1)B+跟B树不同B+树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加;
(2)B+树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样;
(3)B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
(4)非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料 这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现);
1、B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
2、B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定;
3、B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
4、B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是,如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字其数据的地址,所以这种数据检索的时候会要比B+树快。
B*树是B+树的变种,相对于B+树他们的不同之处如下:
(1)首先是关键字个数限制问题,B+树初始化的关键字初始化个数是cei(m/2),b*树的初始化个数为(cei(2/3*m))
(2)B+树节点满时就会分裂,而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移关键字,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来;
在B+树的基础上因其初始化的容量变大,使得节点空间使用率更高,而又存有兄弟节点的指针,可以向兄弟节点转移关键字的特性使得B*树额分解次数变得更少;
1、节点分为红色或者黑色。
2、根节点必为黑色。
3、叶子节点都为黑色,且为 null。
4、连接红色节点的两个子节点都为黑色(红黑树不会出现相邻的红色节点)。
5、从任意节点出发,到其每个叶子节点的路径中包含相同数量的黑色节点。
6、新加入到红黑树的节点为红色节点。
规则看着好像挺多,没错,因为红黑树也是均衡二叉树,需要具备自动维持平衡的性质,上面的6条就是红黑树给出的自动维持平衡所需要具备的规则。
典型的红黑树
①从根节点到叶子节点的最长路径不大于最短路径的 2 倍
怎么样的路径算最短路径?从规则 5 中,我们知道从根节点到每个叶子节点的黑色节点数量是一样的,那么纯由黑色节点组成的路径就是最短路径。
什么样的路径算是最长路径?根据规则 4 和规则 3,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点数量相同时,就是最长路径,
也就是黑色节点(或红色节点)*2。
②为什么说新加入到红黑树中的节点为红色节点
从规则 4 中知道,当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的,此时假如新的是黑色节点的话,必然破坏规则。
但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些。
什么情况下,红黑树的结构会被破坏呢?破坏后又怎么维持平衡,维持平衡主要通过两种方式【变色】和【旋转】,【旋转】又分【左旋】和【右旋】,两种方式可相互结合。 下面我们从插入和删除两种场景来举例说明。
当我们插入值为 66 的节点时,红黑树变成了这样:
很明显,这个时候结构依然遵循着上述6大规则,无需启动自动平衡机制调整节点平衡状态。 如果再向里面插入值为 51 的节点,这个时候红黑树变成了这样:
很明显现在的结构不遵循规则 4 了,这个时候就需要启动自动平衡机制调整节点平衡状态。
变色:我们可以通过变色的方式,使结构满足红黑树的规则:
首先解决结构不遵循规则 4 这一点(红色节点相连,节点 49-51),需将节点 49 改为黑色。
此时我们发现又违反了规则 5(56-49-51-XX 路径中黑色节点超过了其他路径),那么我们将节点 45 改为红色节点。
哈哈,妹的,又违反了规则 4(红色节点相连,节点 56-45-43),那么我们将节点 56 和节点 43 改为黑色节点。
但是我们发现此时又违反了规则 5(60-56-XX 路径的黑色节点比 60-68-XX 的黑色节点多),因此我们需要调整节点 68 为黑色。
完成!
最终调整完成后的树为:
但并不是什么时候都那么幸运,可以直接通过变色就达成目的,大多数时候还需要通过旋转来解决。 如在下面这棵树的基础上,加入节点 65:
插入节点 65 后进行以下步骤:
这个时候,你会发现对于节点64无论是红色节点还是黑色节点,都会违反规则5,路径中的黑色节点始终无法达成一致,这个时候仅通过【变色】已经无法达成目的。
我们需要通过旋转操作,当然【旋转】操作一般还需要搭配【变色】操作。旋转包括【左旋】和【右旋】。
左旋:逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点。
左旋操作步骤如下:首先断开节点PL与右子节点G的关系,同时将其右子节点的引用指向节点C2;
然后断开节点G与左子节点C2的关系,同时将G的左子节点的应用指向节点 PL。
右旋:顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点。
右旋操作步骤如下:首先断开节点 G 与左子节点 PL 的关系,同时将其左子节点的引用指向节点 C2;然后断开节点 PL 与右子节点 C2 的关系,同时将 PL 的右子节点的应用指向节点 G。
无法通过变色而进行旋转的场景分为以下四种:
第一种:左左节点旋转(LL旋转-右单旋转:左(节点)子树的左(子树)节点插入节点)
这种情况下,父节点和插入的节点都是左节点,如下图(旋转原始图1)这种情况下,我们要插入节点 65。
规则如下:以祖父节点【右旋】,搭配【变色】。
按照规则,步骤如下:
第二种:左右节点旋转(LR旋转-先左后右:左(节点)子树的右(子树)节点插入节点)
这种情况下,父节点是左节点,插入的节点是右节点,在旋转原始图 1 中,我们要插入节点 67。
规则如下:先父节点【左旋】,然后祖父节点【右旋】,搭配【变色】。
按照规则,步骤如下:
第三种:右左节点旋转(RL旋转-先右后左:右(节点)子树的左(子树)节点插入节点)
这种情况下,父节点是右节点,插入的节点是左节点,如下图(旋转原始图 2)这种情况,我们要插入节点 68。
规则如下:先父节点【右旋】,然后祖父节点【左旋】,搭配【变色】。
第四种:右右节点旋转(RR旋转-左单旋转:右(节点)子树的右(子树)节点插入节点)
这种情况下,父节点和插入的节点都是右节点,在旋转原始图 2 中,我们要插入节点 70。
规则如下:以祖父节点【左旋】,搭配【变色】。
按照规则,步骤如下:
相比较于红黑树的节点插入,删除节点更为复杂,我们从子节点是否为 null 和红色为思考维度来讨论。
子节点至少有一个为 null
当待删除的节点的子节点至少有一个为 null 节点时,删除了该节点后,将其有值的节点取代当前节点即可。
若都为 null,则将当前节点设置为 null,当然如果违反规则了,则按需调整,如【变色】以及【旋转】。
子节点都是非 null 节点
这种情况下:
第一步:找到该节点的前驱或者后继。
前驱:左子树中值最大的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
后继:右子树中值最小的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
前驱和后继都是值最接近该节点值的节点,类似于该节点.prev=前驱,该节点.next=后继。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继。
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继。
这相当于是一种“取巧”的方法,我们删除节点的目的是使该节点的值在红黑树上不存在。
因此专注于该目的,我们并不关注删除节点时是否真是我们想删除的那个节点,同时我们也不需考虑树结构的变化,因为树的结构本身就会因为自动平衡机制而经常进行调整。
前面我们已经说了,我们要删除的实际上是前驱或者后继,因此我们就以前驱为主线来讲解。
后继的学习可参考前驱,包括下面几种情况:
①前驱为黑色节点,并且有一个非 null 子节点
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63;
删除前驱 63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则 4,因此需要进行自动平衡调整。这里直接通过【变色】即可完成。
②前驱为黑色节点,同时子节点都为 null
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63 替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63。
删除前驱 63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则 5,因此需要进行自动平衡调整。这里直接通过【变色】即可完成。
③前驱为红色节点,同时子节点都为 null
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63;删除前驱 63,树的结构并没有打破规则。
红黑树删除的情况比较多,但也就存在以下情况:
删除的是根节点,则直接将根节点置为 null。
待删除节点的左右子节点都为 null,删除时将该节点置为 null。
待删除节点的左右子节点有一个有值,则用有值的节点替换该节点即可。
待删除节点的左右子节点都不为 null,则找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继。
节点删除后可能会造成红黑树的不平衡,这时我们需通过【变色】+【旋转】的方式来调整,使之平衡,上面也给出了例子,建议大家多多练习,而不必背下来。
本文主要介绍了红黑树的相关原理,首先红黑树的基础二叉搜索树,我们先简单说了一下二叉搜索树,并且讲了一下搜索的流程。
然后就针对红黑树的六大规则特点,红黑树的插入操作,删除操作,都使用了大量的图形来加以说明。
红黑树的使用非常广泛,如 TreeMap 和 TreeSet 都是基于红黑树实现的,而 JDK8 中 HashMap 当链表长度大于 8 时也会转化为红黑树。
单链表中查询一个元素的时间复杂度为O(n),即使该单链表是有序的,我们也不能通过2分的方式缩减时间复杂度。
如上图,我们要查询元素为55的结点,必须从头结点,循环遍历到最后一个节点,不算-INF(负无穷)一共查询8次。那么用什么办法能够用更少的次数访问55呢?最直观的,当然是新开辟一条捷径去访问55。
如上图,我们要查询元素为55的结点,只需要在L2层查找4次即可。在这个结构中,查询结点为46的元素将耗费最多的查询次数5次。即先在L2查询46,查询4次后找到元素55,因为链表是有序的,46一定在55的左边,所以L2层没有元素46。然后我们退回到元素37,到它的下一层即L1层继续搜索46。非常幸运,我们只需要再查询1次就能找到46。这样一共耗费5次查询。
那么,如何才能更快的搜寻55呢?有了上面的经验,我们就很容易想到,再开辟一条捷径。
如上图,我们搜索55只需要2次查找即可。这个结构中,查询元素46仍然是最耗时的,需要查询5次。即首先在L3层查找2次,然后在L2层查找2次,最后在L1层查找1次,共5次。很显然,这种思想和2分非常相似,那么我们最后的结构图就应该如下图。
我们可以看到,最耗时的访问46需要6次查询。即L4访问55,L3访问21、55,L2访问37、55,L1访问46。我们直觉上认为,这样的结构会让查询有序链表的某个元素更快。那么究竟算法复杂度是多少呢?
如果有n个元素,因为是2分,所以层数就应该是log n层 (本文所有log都是以2为底),再加上自身的1层。以上图为例,如果是4个元素,那么分层为L3和L4,再加上本身的L2,一共3层;如果是8个元素,那么就是3+1层。最耗时间的查询自然是访问所有层数,耗时logn+logn,即2logn。为什么是2倍的logn呢?我们以上图中的46为例,查询到46要访问所有的分层,每个分层都要访问2个元素,中间元素和最后一个元素。所以时间复杂度为O(logn)。
至此为止,我们引入了最理想的跳跃表,但是如果想要在上图中插入或者删除一个元素呢?比如我们要插入一个元素22、23、24……,自然在L1层,我们将这些元素插入在元素21后,那么L2层,L3层呢?我们是不是要考虑插入后怎样调整连接,才能维持这个理想的跳跃表结构。我们知道,平衡二叉树的调整是一件令人头痛的事情,左旋右旋左右旋……一般人还真记不住,而调整一个理想的跳跃表将是一个比调整平衡二叉树还复杂的操作。幸运的是,我们并不需要通过复杂的操作调整连接来维护这样完美的跳跃表。有一种基于概率统计的插入算法,也能得到时间复杂度为O(logn)的查询效率,这种跳跃表才是我们真正要实现的。
单链表的查找时间复杂度为:O(n),下面分析下跳表这种数据结构的查找时间复杂度:
我们首先考虑这样一个问题,如果链表里有n个结点,那么会有多少级索引呢?按照上面讲的,每两个结点都会抽出一个结点作为上一级索引的结点。那么第一级索引的个数大约就是N/2,第二级的索引大约就是N/4,第三级的索引就是N/8,依次类推,也就是说,第k级索引的结点个数是第k-1级索引的结点个数的1/2,那么第k级的索引结点个数为:N/(2^k)
假设索引有h级,最高级的索引有2个结点,通过上面的公式,我们可以得到h=logN-1,如果包含原始链表这一层,整个跳表的高度就是logN,我们在跳表中查找某个数据的时候,如果每一层都要遍历m个结点,那么在跳表中查询一个数据的时间复杂度就为:O(m*logN)。
其实根据前面的分析,我们不难得出m=3,即每一级索引都最多只需要遍历3个结点,分析如下:
如上图所示,假如我们要查找的数据是x,在第k级索引中,我们遍历到y结点之后,发现x大于y,小于y后面的结点z。所以我们通过y的down指针,从第k级索引下降到第k-1级索引。在第k-1级索引中,y和z之间只有3个结点(包含y和z)。所以,我们在k-1级索引中最多需要遍历3个结点,以此类推,每一级索引都最多只需要遍历3个结点。
因此,m=3,所以跳表查找任意数据的时间复杂度为O(logn),这个查找的时间复杂度和二分查找是一样的,但是我们却是基于单链表这种数据结构实现的。不过,天下没有免费的午餐,这种查找效率的提升是建立在很多级索引之上的,即空间换时间的思想。
比起单纯的单链表,跳表就需要额外的存储空间去存储多级索引。假设原始链表的大小为n,那么第一级索引大约有n/2个结点,第二级索引大约有4/n个结点,依次类推,每上升一级索引结点的个数就减少一半,直到剩下最后2个结点,如下图所示,其实就是一个等比数列。

其实从上面的分析,我们利用空间换时间的思想,已经把时间压缩到了极致,因为每一级每两个索引结点就有一个会被抽到上一级的索引结点中,所以此时跳表所需要的额外内存空间最多,即空间复杂度最高。其实我们可以通过改变抽取结点的间距来降低跳表的空间复杂度,在其时间复杂度和空间复杂度方面取一个综合性能,当然也要看具体情况,如果内存空间足够,那就可以选择最小的结点间距,即每两个索引结点抽取一个结点到上一级索引中。如果想降低跳表的空间复杂度,则可以选择每三个或者每五个结点,抽取一个结点到上级索引中。
如上图所示,每三个结点抽取一个结点到上一级索引中,则第一级需要大约n/3个结点,第二级索引大约需要n/9个结点。每往上一级,索引的结点个数就除以3,为了方便计算,我们假设最高一级的索引结点个数为1,则可以得到一个等比数列。
通过等比数列的求和公式,总的索引结点大约是:n/3 + n /9 + n/27 + ... + 9 + 3 + 1 = n/2。尽管空间复杂度还是O(n),但是比之前的每两个结点抽一个结点的索引构建方法,可以减少了一半的索引结点存储空间。
实际上,在软件开发中,我们不必太在意索引占用的额外空间。在讲数据结构的时候,我们习惯性地把要处理的数据看成整数,但是在实际的软件开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
跳表插入的时间复杂度为:O(logn),支持高效的动态插入。
在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是O(1)。但是为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找的操作就会比较耗时。
对于纯粹的单链表,需要遍历每个结点,来找到插入的位置。但是对于跳表来说,查找的时间复杂度为O(logn),所以这里查找某个数据应该插入的位置的时间复杂度也是O(logn),如下图所示:
跳表的删除操作时间复杂度为:O(logn),支持动态的删除。
在跳表中删除某个结点时,如果这个结点在索引中也出现了,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到删除结点的前驱结点,然后再通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点(双向链表除外)。因此跳表的删除操作时间复杂度即为O(logn)。
当我们不断地往跳表中插入数据时,我们如果不更新索引,就有可能出现某2个索引节点之间的数据非常多的情况,在极端情况下,跳表还会退化成单链表
作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中的结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入和删除操作性能的下降。
如果你了解红黑树、AVL树这样的平衡二叉树,你就会知道它们是通过左右旋的方式保持左右子树的大小平衡,而跳表是通过随机函数来维护“平衡性”。
当我们往跳表中插入数据的时候,我们可以通过一个随机函数,来决定这个结点插入到哪几级索引层中,比如随机函数生成了值K,那我们就将这个结点添加到第一级到第K级这个K级索引中。如下图中要插入数据为6,K=2的例子
随机函数的选择是非常有讲究的,从概率上讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能的过度退化。
(1) 由很多层结构组成,level是通过一定的概率随机产生的;
(2) 每一层都是一个有序的链表,默认是升序 ;
(3) 最底层(Level 1)的链表包含所有元素;
(4) 如果一个元素出现在Level i 的链表中,则它在Level i 之下的链表也都会出现;
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面
先讨论插入,我们先看理想的跳跃表结构,L2层的元素个数是L1层元素个数的1/2,L3层的元素个数是L2层的元素个数的1/2,以此类推。从这里,我们可以想到,只要在插入时尽量保证上一层的元素个数是下一层元素的1/2,我们的跳跃表就能成为理想的跳跃表。那么怎么样才能在插入时保证上一层元素个数是下一层元素个数的1/2呢?很简单,抛硬币就能解决了!假设元素X要插入跳跃表,很显然,L1层肯定要插入X。那么L2层要不要插入X呢?我们希望上层元素个数是下层元素个数的1/2,所以我们有1/2的概率希望X插入L2层,那么抛一下硬币吧,正面就插入,反面就不插入。那么L3到底要不要插入X呢?相对于L2层,我们还是希望1/2的概率插入,那么继续抛硬币吧!以此类推,元素X插入第n层的概率是(1/2)的n次。这样,我们能在跳跃表中插入一个元素了。
在此还是以上图为例:跳跃表的初试状态如下图,表中没有一个元素:
然后我们抛硬币,结果是正面,那么我们要将2插入到L2层,如下图:
继续抛硬币,结果是反面,那么元素2的插入操作就停止了,插入后的表结构就是上图所示。接下来,我们插入元素33,跟元素2的插入一样,现在L1层插入33,如下图:
然后抛硬币,结果是反面,那么元素33的插入操作就结束了,插入后的表结构就是上图所示。接下来,我们插入元素55,首先在L1插入55,插入后如下图:
以此类推,我们插入剩余的元素。当然因为规模小,结果很可能不是一个理想的跳跃表。但是如果元素个数n的规模很大,学过概率论的同学都知道,最终的表结构肯定非常接近于理想跳跃表。
当然,这样的分析在感性上是很直接的,但是时间复杂度的证明实在复杂,在此我就不深究了,感兴趣的可以去看关于跳跃表的paper。再讨论删除,删除操作没什么讲的,直接删除元素,然后调整一下删除元素后的指针即可。跟普通的链表删除操作完全一样。再来讨论一下时间复杂度,插入和删除的时间复杂度就是查询元素插入位置的时间复杂度,这不难理解,所以是O(logn)。
代码实现见 com.structure.simple.SkipListDemo
(1)Redis中的有序集合是通过跳表来实现的,当然还用到了散列表。
(2)大部分编程语言中的Map类型都是通过红黑树实现的,我们在写程序的时候,可以直接拿过来用,不用自己再去实现一个红黑树。但是跳表并没有一个现成的实现,所以在开发中,如果要使用跳表这种数据结构,需要自己先去实现。
(3)Lucene, elasticSearch
执行步骤:
1、首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2、再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3、重复第二步,直到所有元素均排序完毕。
时间复杂度:
选择排序的交换操作介于 0 和 (n - 1)次之间。选择排序的比较操作为 n (n - 1) / 2 次之间。
选择排序的赋值操作介于 0 和 3 (n - 1) 次之间。比较次数O(n^2),比较次数与关键字的初始状态无关,
总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。交换次数O(n),最好情况是,已经有序,交换0次;
最坏情况交换n-1次,逆序交换n/2次。交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,
n值较小时,选择排序比冒泡排序快。
稳定性:
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,
依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,
如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,
所以选择排序是一个不稳定的排序算法。
执行步骤:
1、比较相邻的元素,如果前一个比后一个大,交换之。
2、第一趟排序第1个和第2个一对,比较与交换,随后第2个和第3个一对比较交换,这样直到倒数第2个和最后1个,将最大的数移动到最后一位。
3、第二趟将第二大的数移动至倒数第二位...... 因此需要n-1趟;
时间复杂度:
若文件的初始状态是正序的,一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值:Cmin = n-1,Mmin = 0
所以,冒泡排序最好的时间复杂度为O(n)。若初始文件是反序的,需要进行n-1趟排序。
每趟排序要进行n-i次关键字的比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
Cmax = n(n-1)/2 = O(n^2) Mmax = 3n(n-1)/2 = O(n^2)冒泡排序的最坏时间复杂度为O(n^2)。
综上,因此冒泡排序总的平均时间复杂度为O(n^2)。
算法稳定性:
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,
是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,
所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
执行步骤:
1、假设前面 n-1(其中 n>=2)个数已经是排好顺序的,现将第 n 个数插到前面已经排好的序列中,然后找到合适自己的位置,
使得插入第n个数的这个序列也是排好顺序的。
2、按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
时间复杂度:
在插入排序中,当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较N- 1次,时间复杂度为O(n)。
最坏的情况是待排序数组是逆序的,此时需要比较次数最多,总次数记为:1+2+3+…+N-1,所以,插入排序最坏情况下的时间复杂度为O(n^2)。
平均来说,A[1..j-1]中的一半元素小于A[j],一半元素大于A[j]。插入排序在平均情况运行时间与最坏情况运行时间一样,是输入规模的二次函数。
空间复杂度:插入排序的空间复杂度为常数阶O(1)
稳定性分析:
如果待排序的序列中存在两个或两个以上具有相同关键词的数据,排序后这些数据的相对次序保持不变,即它们的位置保持不变,
通俗地讲,就是两个相同的数的相对顺序不会发生改变,则该算法是稳定的;如果排序后,数据的相对次序发生了变化,则该算法是不稳定的。
关键词相同的数据元素将保持原有位置不变,所以该算法是稳定的
执行流程:
1、申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2、设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4、重复步骤3直到某一指针达到序列尾;
5、将另一序列剩下的所有元素直接复制到合并序列尾。
复杂度
归并排序比较占用内存,但却是一种效率高且稳定的算法。
改进归并排序在归并时先判断前段序列的最大值与后段序列最小值的关系再确定是否进行复制比较。如果前段序列的最大值小于等于后段序列最小值,
则说明序列可以直接形成一段有序序列不需要再归并,反之则需要。所以在序列本身有序的情况下时间复杂度可以降至O(n)
TimSort可以说是归并排序的终极优化版本,主要思想就是检测序列中的天然有序子段(若检测到严格降序子段则翻转序列为升序子段)。
在最好情况下无论升序还是降序都可以使时间复杂度降至为O(n),具有很强的自适应性。
**** 最好时间复杂度 最坏时间复杂度 平均时间复杂度 空间复杂度 稳定性
传统归并排序 O(nlogn) O(nlogn) O(nlogn) T(n) 稳定
改进归并排序 O(n) O(nlogn) O(nlogn) T(n) 稳定
TimSort O(n) O(nlogn) O(nlogn) T(n) 稳定
Master表达式推导
T(N) = a*T(N/b) + O(N^d)
1) log(b,a) > d 时间复杂度为 O(N^log(b,a))
2) log(b,a) = d 时间复杂度为 O(N^d * logN)
3) log(b,a) < d 时间复杂度为 O(N^d)
归并排序可通过该表达式推出时间复杂度
仅查看递归方法 {@link InsertSortDemo#process} 的一层即可,不需要看递归多层计算
可得 Master 表达式为
T(N) = 2 * T(N/2) + O(N^1)
a = 2, b = 2,d = 1
log(2,2) = 1
可得出时间复杂度为 O(N * logN)
执行流程:
1、取中间位置的值与目标值进行比对
2、若目标值大于(小于)中间值,则从数组右侧(左侧)中查找。否则则从数组左侧(右侧)中进行查找
3、重复执行1、2步骤,直到运行完成
复杂度:
由于开始比较都是从最中间位置的数组值进行比较,所以树的高度h总是维持在 O(logN) 或 O(logN)+1。
所以每次搜索目标值是最差的情况下,时间复杂度为O(logN)
执行流程:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
演示示例:
假设一开始序列{xi}是:5,3,7,6,4,1,0,2,9,10,8。
此时,ref=5,i=1,j=11,从后往前找,第一个比5小的数是x8=2,因此序列为:2,3,7,6,4,1,0,5,9,10,8。
此时i=1,j=8,从前往后找,第一个比5大的数是x3=7,因此序列为:2,3,5,6,4,1,0,7,9,10,8。
此时,i=3,j=8,从第8位往前找,第一个比5小的数是x7=0,因此:2,3,0,6,4,1,5,7,9,10,8。
此时,i=3,j=7,从第3位往后找,第一个比5大的数是x4=6,因此:2,3,0,5,4,1,6,7,9,10,8。
此时,i=4,j=7,从第7位往前找,第一个比5小的数是x6=1,因此:2,3,0,1,4,5,6,7,9,10,8。
此时,i=4,j=6,从第4位往后找,直到第6位才有比5大的数,这时,i=j=6,ref成为一条分界线,它之前的数都比它小,之后的数都比它大,对于前后两部分数,可以采用同样的方法来排序。
复杂度:
快速排序的一次划分算法从两头交替搜索,直到low和hight重合,因此其时间复杂度是O(n);而整个快速排序算法的时间复杂度与划分的趟数有关。
理想的情况是,每次划分所选择的中间数恰好将当前序列几乎等分,经过log2n趟划分,便可得到长度为1的子表。这样,整个算法的时间复杂度为O(nlog2n)。
最坏的情况是,每次所选的中间数是当前序列中的最大或最小元素,这使得每次划分所得的子表中一个为空表,另一子表的长度为原表的长度-1。这样,长度为n的数据表的快速排序需要经过n趟划分,使得整个排序算法的时间复杂度为O(n2)。
为改善最坏情况下的时间性能,可采用其他方法选取中间数。通常采用“三者值取中”方法,即比较H->r[low].key、H->r[high].key与H->r[(low+high)/2].key,取三者中关键字为中值的元素为中间数。
可以证明,快速排序的平均时间复杂度也是O(nlog2n)。因此,该排序方法被认为是目前最好的一种内部排序方法。
从空间性能上看,尽管快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归。最好的情况下,即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表,所需栈的最大深度为log2(n+1);但最坏的情况下,栈的最大深度为n。这样,快速排序的空间复杂度为O(log2n)。
当你往简单数组或列表中插入新数据时,将不会根据插入项的值来确定该插入项的索引值。 这意味着新插入项的索引值与数据值之间没有直接关系。这样的话, 当你需要在数组或列表中搜索相应值的时候,你必须遍历已有的集合。 若集合中存在大量的数据,就会影响数据查找的效率。 针对这个问题,你可以考虑使用哈希表。利用哈希表你可以通过对 “值” 进行哈希处理来获得该值对应的键或索引值,然后把该值存放到列表中对应的索引位置。 这意味着索引值是由插入项的值所确定的,当你需要判断列表中是否存在该值时, 只需要对值进行哈希处理并在相应的索引位置进行搜索即可,这时的搜索速度是非常快的。
根据定义,布隆过滤器可以检查值是 “可能在集合中” 还是 “绝对不在集合中”。“可能” 表示有一定的概率,也就是说可能存在一定为误判率。那为什么会存在误判呢? 下面我们来分析一下具体的原因。布隆过滤器(Bloom Filter)本质上是由长度为 m 的位向量或位列表(仅包含 0 或 1 位值的列表)组成, 最初所有的值均设置为 0,如下图所示。
为了将数据项添加到布隆过滤器中,我们会提供 K 个不同的哈希函数,并将结果位置上对应位的值置为 “1”。在前面所提到的哈希表中, 我们使用的是单个哈希函数,因此只能输出单个索引值。而对于布隆过滤器来说,我们将使用多个哈希函数,这将会产生多个索引值。
如上图所示,当输入 “semlinker” 时,预设的 3 个哈希函数将输出 2、4、6,我们把相应位置 1。假设另一个输入 ”kakuqo“,哈希函数输出 3、4 和 7。 你可能已经注意到,索引位 4 已经被先前的 “semlinker” 标记了。 此时,我们已经使用 “semlinker” 和 ”kakuqo“ 两个输入值,填充了位向量。当前位向量的标记状态为:
当对值进行搜索时,与哈希表类似,我们将使用 3 个哈希函数对 ”搜索的值“ 进行哈希运算,并查看其生成的索引值。假设,当我们搜索 ”fullstack“ 时, 3 个哈希函数输出的 3 个索引值分别是 2、3 和 7:
从上图可以看出,相应的索引位都被置为 1,这意味着我们可以说 ”fullstack“ 可能已经插入到集合中。事实上这是误报的情形, 产生的原因是由于哈希碰撞导致的巧合而将不同的元素存储在相同的比特位上。幸运的是,布隆过滤器有一个可预测的误判率(FPP):
n 是已经添加元素的数量;
k 哈希的次数;
m 布隆过滤器的长度(如比特数组的大小)
极端情况下,当布隆过滤器没有空闲空间时(满),每一次查询都会返回 true 。这也就意味着 m 的选择取决于期望预计添加元素的数量 n ,并且 m 需要远远大于 n 。 实际情况中,布隆过滤器的长度 m 可以根据给定的误判率(FFP)的和期望添加的元素个数 n 的通过如下公式计算:
了解完上述的内容之后,我们可以得出一个结论,当我们搜索一个值的时候,若该值经过 K 个哈希函数运算后的任何一个索引位为 ”0“,那么该值肯定不在集合中。 但如果所有哈希索引值均为 ”1“,则只能说该搜索的值可能存在集合中。
①在实际工作中,布隆过滤器常见的应用场景如下:
②网页爬虫对 URL 去重,避免爬取相同的 URL 地址;
③反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
④Google Chrome 使用布隆过滤器识别恶意 URL;
⑤Medium 使用布隆过滤器避免推荐给用户已经读过的文章;
⑥Google BigTable,Apache HBbase 和 Apache Cassandra 使用布隆过滤器减少对不存在的行和列的查找。
除了上述的应用场景之外,布隆过滤器还有一个应用场景就是解决缓存穿透的问题。所谓的缓存穿透就是服务调用方每次都是查询不在缓存中的数据,
这样每次服务调用都会到数据库中进行查询,如果这类请求比较多的话,就会导致数据库压力增大,这样缓存就失去了意义。
漏桶算法思路很简单,请求先进入到漏桶里,漏桶以固定的速度出水,也就是处理请求,当水加的过快,则会直接溢出,也就是拒绝请求,可以看出漏桶算法能强行限制数据的传输速率。

该算法很好的解决了时间边界处理不够平滑的问题,因为在每次请求进桶前都将执行“漏水”的操作,再无边界问题。
但是对于很多场景来说,除了要求能够限制数据的平均传输速率外,还要求允许某种程度的突发传输。这时候漏桶算法可能就不合适了,令牌桶算法更为适合。
令牌桶算法的原理是系统会以一个恒定的速度往桶里放入令牌,而如果请求需要被处理,则需要先从桶里获取一个令牌,当桶里没有令牌可取时,则拒绝服务。
令牌桶是网络设备的内部存储池,而令牌则是以给定速率填充令牌桶的虚拟信息包。每个到达的令牌都会从数据队列领出相应的数据包进行发送,发送完数据后令牌被删除。
请求注解(RFC)中定义了两种令牌桶算法——单速率三色标记算法和双速率三色标记算法,其评估结果都是为报文打上红、黄、绿三色标记。QoS会根据报文的颜色,设置报文的丢弃优先级,其中单速率三色标记比较关心报文尺寸的突发,而双速率三色标记则关注速率上的突发,两种算法都可工作于色盲模式和非色盲模式。以下结合这两种工作模式介绍一下RFC中所描述的这两种算法。
1)单速率三色标记算法
网络工程师任务小组(IETF)的RFC文件定义了单速率三色标记算法,评估依据以下3个参数:承诺访问速率(CIR),即向令牌桶中填充令牌的速率;承诺突发尺寸(CBS),即令牌桶的容量,每次突发所允许的最大流量尺寸(注:设置的突发尺寸必须大于最大报文长度);超额突发尺寸(EBS)。
一般采用双桶结构:C桶和E桶。Tc表示C桶中的令牌数,Te表示E桶中令牌数,两桶的总容量分别为CBS和EBS。初始状态时两桶是满的,即Tc和Te初始值分别等于CBS和EBS。令牌的产生速率是CIR,通常是先往C桶中添加令牌,等C桶满了,再往E桶中添加令牌,当两桶都被填满时,新产生的令牌将会被丢弃。
色盲模式下,假设到达的报文长度为B。若报文长度B小于C桶中的令牌数Tc,则报文被标记为绿色,且C桶中的令牌数减少B;若Tc<B <Te,则标记为黄色,E和C桶中的令牌数均减少B;若B >Te,标记为红色,两桶总令牌数都不减少。
在非色盲模式下,若报文已被标记为绿色或B <Tc,则报文被标记为绿色,Tc减少B;若报文已被标记为黄色或Tc<B <Te,则标记为黄色,且Te减少B;若报文已被标记为红色或B >Te,则标记为红色,Tc和Te都不减少。
注意:
①色盲模式下,当报文长度B大于Tc且小于Te(即Tc<B<Te)时,E桶与C桶中令牌数均减少B个。而非色盲情况下,Tc<B<Te时仅E桶减少B个令牌数
②B<Tc,绿色。Tc<B<Te时,黄色。 B>Te,红色。
③优先级:绿<黄<红
2)双速率三色标记算法
IETF的RFC文件定义了双速率三色算法,主要是根据4种流量参数来评估:CIR、CBS、峰值信息速率(PIR),峰值突发尺寸(PBS)。前两种参数与单速率三色算法中的含义相同,PIR这个参数只在交换机上才有,路由器没有这个参数。该值必须不小于CIR的设置值,如果大于CIR,则速率限制在CIR于PRI之间的一个值。
与单速率三色标记算法不同,双速率三色标记算法的两个令牌桶C桶和P桶填充令牌的速率不同,C桶填充速率为CIR,P桶为PIR;两桶的容量分别为CBS和PBS。用Tc和Tp表示两桶中的令牌数目,初始状态时两桶是满的,即Tc和Tp初始值分别等于CBS和PBS。
色盲模式下,如果到达的报文速率大于PIR,超过Tp+Tc部分无法得到令牌,报文被标记为红色,未超过Tp+Tc而从P桶中获取令牌的报文标记为黄色,从C桶中获取令牌的报文被标记为绿色;当报文速率小于PIR,大于CIR时,报文不会得不到令牌,但超过Tp部分报文将从P桶中获取令牌,被标记为黄色报文,从C桶中获取令牌的报文被标记为绿色;当报文速率小于CIR时,报文所需令牌数不会超过Tc,只从C桶中获取令牌,所以只会被标记为绿色报文。
在非色盲模式下,如果报文已被标记为红色或者超过Tp+Tc部分无法得到令牌的报文,被标记为红色;如果标记为黄色或者超过Tc未超过Tp部分报文记为黄色;如果报文被标记为绿或未超过Tc部分报文,被标记为绿色。
1)假如用户配置的平均发送速率为r,则每隔1/r秒一个令牌被加入到桶中(每秒会有r个令牌放入桶中);
2)假设桶中最多可以存放b个令牌。如果令牌到达时令牌桶已经满了,那么这个令牌会被丢弃;
3)当一个n个字节的数据包到达时,就从令牌桶中删除n个令牌(不同大小的数据包,消耗的令牌数量不一样),并且数据包被发送到网络;
如果令牌桶中少于n个令牌,那么不会删除令牌,并且认为这个数据包在流量限制之外(n个字节,需要n个令牌。该数据包将被缓存或丢弃);
4)算法允许最长b个字节的突发,但从长期运行结果看,数据包的速率被限制成常量r。对于在流量限制外的数据包可以以不同的方式处理:
①它们可以被丢弃;
②它们可以排放在队列中以便当令牌桶中累积了足够多的令牌时再传输;
③它们可以继续发送,但需要做特殊标记,网络过载的时候将这些特殊标记的包丢弃。
两者主要区别在于“漏桶算法”能够强行限制数据的传输速率,而“令牌桶算法”在能够限制数据的平均传输速率外,还允许某种程度的突发传输。在“令牌桶算法”中,只要令牌桶中存在令牌,那么就允许突发地传输数据直到达到用户配置的门限,所以它适合于具有突发特性的流量。
服务降级算法是采用令牌桶算法。并不能说明令牌桶一定比漏桶好,她们使用场景不一样。令牌桶可以用来保护自己,主要用来对调用者频率进行限流,
为的是让自己不被打垮。所以如果自己本身有处理能力的时候,如果流量突发(实际消费能力强于配置的流量限制),
那么实际处理速率可以超过配置的限制。而漏桶算法,这是用来保护他人,也就是保护他所调用的系统。主要场景是,当调用的第三方系统本身没有保护机制,
或者有流量限制的时候,我们的调用速度不能超过他的限制,由于我们不能更改第三方系统,所以只有在主调方控制。这个时候,即使流量突发,也必须舍弃。
因为消费能力是第三方决定的。总结起来:如果要让自己的系统不被打垮,用令牌桶。如果保证别人的系统不被打垮,用漏桶算法
参考:https://zhuanlan.zhihu.com/p/165006444
https://www.cnblogs.com/xuwc/p/9123078.html
采用计数器实现限流有点简单粗暴,一般我们会限制一秒钟的能够通过的请求数,比如限流qps为100,算法的实现思路就是从第一个请求进来开始计时,在接下去的1s内,每来一个请求,就把计数加1,如果累加的数字达到了100,那么后续的请求就会被全部拒绝。等到1s结束后,把计数恢复成0,重新开始计数。
TCP协议为控制流量使用滑动窗口法,本节主要讲解滑动窗口在TCP中的应用
TCP滑动窗口分为接收窗口,发送窗口。
滑动窗口协议是传输层进行流控的一种措施,接收方通过发送方自己的窗口大小,从而控制发送方的发送速度,从而达到防止发送方发送速度过快而导致自己被淹没的目的。
对ACK的再认识,ack通常被理解为收到数据后给出的一个确认ACK,ACK包含两个非常重要的信息:
一是期望接收到的下一字节的序号n,该n代表接收方已经接收到了前n-1字节数据,此时如果接收方收到第n+1字节数据而不是第n字节数据,**接收方是不会发送序号为n+2的ACK的。**举个例子,假如接收端收到1-1024字节,它会发送一个确认号为1025的ACK,但是接下来收到的是2049-3072,它是不会发送确认号为3072的ACK,而依旧发送1025的ACK。
二是当前的窗口大小m,如此发送方在接收到ACK包含的这两个数据后就可以计算出还可以发送多少字节的数据给对方,假定当前发送方已发送到第x字节,则可以发送的字节数就是y=m-(x-n).这就是滑动窗口控制流量的基本原理
注意:发送方根据收到ACK当中的期望收到的下一个字节的序号n以及窗口m,还有当前已经发送的字节序号x,算出还可以发送的字节数。
发送端窗口的第一个字节序号一定是ACK中期望收到的下一个字节序号,比如下图:
上图52 53 54 55 字节都是可以新发送的字节序
接收端窗口的第一个字节序之前一定是已经完全接收的,后面窗口里面的数据都是希望接收的,窗口后面的数据都是不希望接收的。
TCP的滑动窗口分为接收窗口和发送窗口,不分析这两种窗口就讨论是不妥当的。TCP的滑动窗口主要有两个作用,一是提供TCP的可靠性,二是提供TCP的流控特性。同时滑动窗口机制还体现了TCP面向字节流的设计思路。TCP 段中窗口的相关字段。
TCP的Window是一个16bit位字段,它代表的是窗口的字节容量,也就是TCP的标准窗口最大为2^16-1=65535个字节。另外在TCP的选项字段中还包含了一个TCP窗口扩大因子,option-kind为3,option-length为3个字节,option-data取值范围0-14。窗口扩大因子用来扩大TCP窗口,可把原来16bit的窗口,扩大为31bit。
1、对于TCP会话的发送方,任何时候在其发送缓存内的数据都可以分为4类,“已经发送并得到对端ACK的”,“已经发送但还未收到对端ACK的”,“未发送但对端允许发送的”,“未发送且对端不允许发送”。“已经发送但还未收到对端ACK的”和“未发送但对端允许发送的”这两部分数据称之为发送窗口。
当收到接收方新的ACK对于发送窗口中后续字节的确认是,窗口滑动,滑动原理如下图。
当收到ACK=36时窗口滑动。
2、对于TCP的接收方,在某一时刻在它的接收缓存内存在3种。“已接收”,“未接收准备接收”,“未接收并未准备接收”(由于ACK直接由TCP协议栈回复,默认无应用延迟,不存在“已接收未回复ACK”)。其中“未接收准备接收”称之为接收窗口。
发送窗口与接收窗口关系
TCP是全双工的协议,会话的双方都可以同时接收、发送数据。TCP会话的双方都各自维护一个“发送窗口”和一个“接收窗口”。其中各自的“接收窗口”大小取决于应用、系统、硬件的限制(TCP传输速率不能大于应用的数据处理速率。各自的“发送窗口”则要求取决于对端通告的“接收窗口”,要求相同。
滑动窗口实现面向流的可靠性
1)最基本的传输可靠性来源于“确认重传”机制。
2)TCP的滑动窗口的可靠性也是建立在“确认重传”基础上的。
3)发送窗口只有收到对端对于本段发送窗口内字节的ACK确认,才会移动发送窗口的左边界。
4)接收窗口只有在前面所有的段都确认的情况下才会移动左边界。当在前面还有字节未接收但收到后面字节的情况下,窗口不会移动,并不对后续字节确认。以此确保对端会对这些数据重传。
滑动窗口的流控特性
TCP的滑动窗口是动态的,我们可以想象成小学常见的一个数学题,一个水池,体积V,每小时进水量V1,出水量V2。当水池满了就不允许再注入了,如果有个液压系统控制水池大小,那么就可以控制水的注入速率和量。这样的水池就类似TCP的窗口。应用根据自身的处理能力变化,通过本端TCP接收窗口大小控制来对对对端的发送窗口流量限制。应用程序在需要(如内存不足)时,通过API通知TCP协议栈缩小TCP的接收窗口。然后TCP协议栈在下个段发送时包含新的窗口大小通知给对端,对端按通知的窗口来改变发送窗口,以此达到减缓发送速率的目的。
Paxos算法在分布式领域具有非常重要的地位。但是Paxos算法有两个比较明显的缺点:1.难以理解 2.工程实现更难。
Paxos算法是基于消息传递且具有高度容错特性的一致性算法,是目前公认的解决分布式一致性问题最有效的算法之一。若想深入研究可查阅《Paxos Made Simple》
在常见的分布式系统中,总会发生诸如机器宕机或网络异常(包括消息的延迟、丢失、重复、乱序,还有网络分区)等情况。Paxos算法需要解决的问题就是如何在一个可能发生上述异常的分布式系统中,快速且正确地在集群内部对某个数据的值达成一致,并且保证不论发生以上任何异常,都不会破坏整个系统的一致性。 注:这里某个数据的值并不只是狭义上的某个数,它可以是一条日志,也可以是一条命令(command)根据应用场景不同,某个数据的值有不同的含义。
在Paxos算法中,有三种角色:Proposer、Acceptor、Learners。
在具体的实现中,一个进程可能同时充当多种角色。比如一个进程可能既是Proposer又是Acceptor又是Learner。还有一个很重要的概念叫提案(Proposal)。最终要达成一致的value就在提案里。
注:
暂且认为『提案=value』,即提案只包含value。在我们接下来的推导过程中会发现如果提案只包含value,会有问题,于是我们再对提案重新设计。
暂且认为『Proposer可以直接提出提案』。在我们接下来的推导过程中会发现如果Proposer直接提出提案会有问题,需要增加一个学习提案的过程。
Proposer可以提出(propose)提案;Acceptor可以接受(accept)提案;如果某个提案被选定(chosen),那么该提案里的value就被选定了。回到刚刚说的『对某个数据的值达成一致』,指的是Proposer、Acceptor、Learner都认为同一个value被选定(chosen)。那么,Proposer、Acceptor、Learner分别在什么情况下才能认为某个value被选定呢?
- Proposer:只要Proposer发的提案被Acceptor接受(刚开始先认为只需要一个Acceptor接受即可,在推导过程中会发现需要半数以上的Acceptor同意才行),Proposer就认为该提案里的value被选定了。
- Acceptor:只要Acceptor接受了某个提案,Acceptor就认为该提案里的value被选定了。
- Learner:Acceptor告诉Learner哪个value被选定,Learner就认为那个value被选定。
假设有一组可以提出(propose)value(value在提案Proposal里)的进程集合。一个一致性算法需要保证提出的这么多value中,只有一个value被选定(chosen)。如果没有value被提出,就不应该有value被选定。如果一个value被选定,那么所有进程都应该能**学习(learn)**到这个被选定的value。对于一致性算法,**安全性(safaty)**要求如下:
- 只有被提出的value才能被选定。
- 只有一个value被选定,并且如果某个进程认为某个value被选定了,那么这个value必须是真的被选定的那个。
我们不去精确地定义其活性(liveness)要求。我们的目标是保证最终有一个提出的value被选定。当一个value被选定后,进程最终也能学习到这个value。 Paxos的目标:保证最终有一个value会被选定,当value被选定后,进程最终也能获取到被选定的value。 假设不同角色之间可以通过发送消息来进行通信,那么:
- 每个角色以任意的速度执行,可能因出错而停止,也可能会重启。一个value被选定后,所有的角色可能失败然后重启,除非那些失败后重启的角色能记录某些信息,否则等他们重启后无法确定被选定的值。
- 消息在传递过程中可能出现任意时长的延迟,可能会重复,也可能丢失。但是消息不会被损坏,即消息内容不会被篡改(拜占庭将军问题)。
最简单方案-只有一个Acceptor
假设只有一个Acceptor(可以有多个Proposer),只要Acceptor接受它收到的第一个提案,则该提案被选定,该提案里的value就是被选定的value。这样就保证只有一个value会被选定。
但是,如果这个唯一的Acceptor宕机了,那么整个系统就无法工作了!因此,必须要有多个Acceptor!

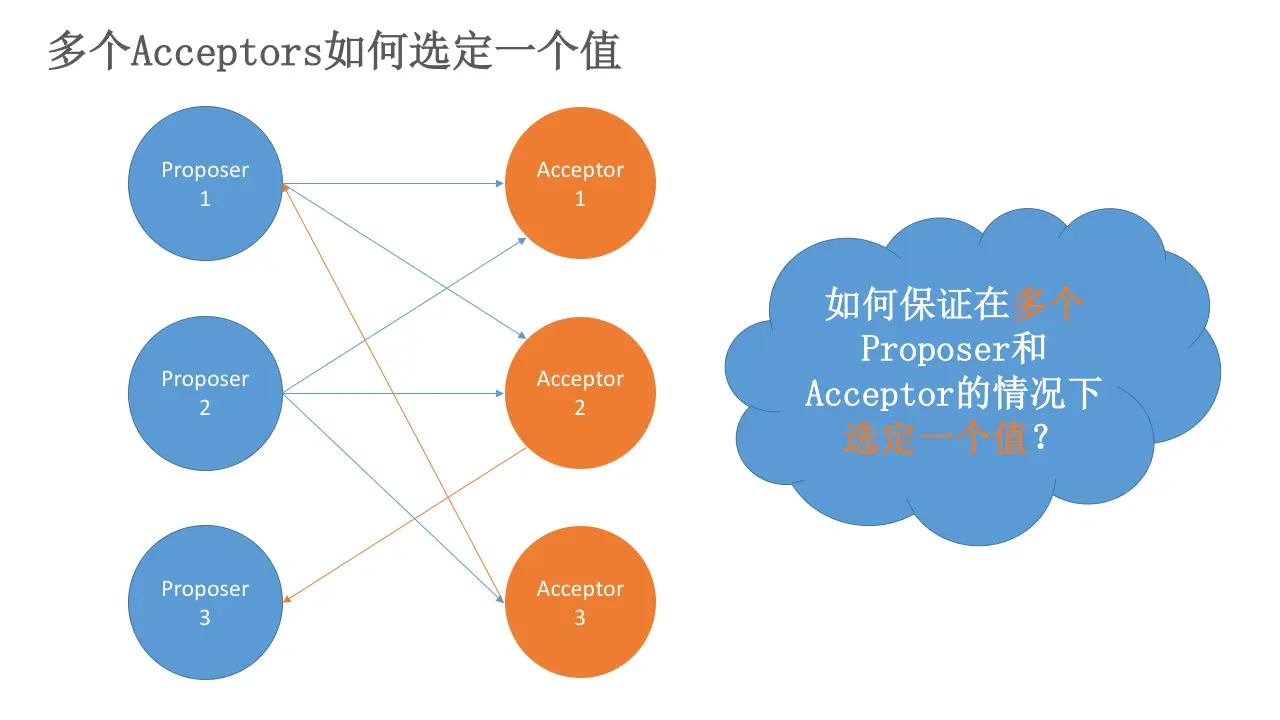
但是,这又会引出另一个问题:如果每个Proposer分别提出不同的value,发给不同的Acceptor。根据P1,Acceptor分别接受自己收到的value,就导致不同的value被选定。出现了不一致。如下图:
刚刚是因为『一个提案只要被一个Acceptor接受,则该提案的value就被选定了』才导致了出现上面不一致的问题。因此,我们需要加一个规定:***(规定)一个提案被选定需要被半数以上的Acceptor接受。***这个规定又暗示了:『一个Acceptor必须能够接受不止一个提案!』不然可能导致最终没有value被选定。比如上图的情况。v1、v2、v3都没有被选定,因为它们都只被一个Acceptor的接受。
最开始讲的『提案=value』已经不能满足需求了,于是重新设计提案,给每个提案加上一个提案编号,表示提案被提出的顺序。令『提案=提案编号+value』。
虽然允许多个提案被选定,但必须保证所有被选定的提案都具有相同的value值。否则又会出现不一致。于是有了下面的约束:(约束P2)如果某个value为v的提案被选定了,那么每个编号更高的被选定提案的value必须也是v。
一个提案只有被Acceptor接受才可能被选定,因此我们可以把P2约束改写成对Acceptor接受的提案的约束P2a。(约束P2a)如果某个value为v的提案被选定了,那么每个编号更高的被Acceptor接受的提案的value必须也是v。
但是,考虑如下的情况:假设总的有5个Acceptor。Proposer2提出[M1,V1]的提案,Acceptor25(半数以上)均接受了该提案,于是对于Acceptor25和Proposer2来讲,它们都认为V1被选定。Acceptor1刚刚从宕机状态恢复过来(之前Acceptor1没有收到过任何提案),此时Proposer1向Acceptor1发送了[M2,V2]的提案(V2≠V1且M2>M1),对于Acceptor1来讲,这是它收到的第一个提案。根据P1(一个Acceptor必须接受它收到的第一个提案。),Acceptor1必须接受该提案!同时Acceptor1认为V2被选定。这就出现了两个问题:
- Acceptor1认为V2被选定,Acceptor2~5和Proposer2认为V1被选定。出现了不一致。
- V1被选定了,但是编号更高的被Acceptor1接受的提案[M2,V2]的value为V2,且V2≠V1。这就跟P2a(如果某个value为v的提案被选定了,那么每个编号更高的被Acceptor接受的提案的value必须也是v)矛盾了。
所以我们要对P2a约束进行强化!P2a是对Acceptor接受的提案约束,但其实提案是Proposer提出来的,所有我们可以对Proposer提出的提案进行约束。得到P2b:(约束P2b)如果某个value为v的提案被选定了,那么之后任何Proposer提出的编号更高的提案的value必须也是v。由P2b可以推出P2a进而推出P2。那么,如何确保在某个value为v的提案被选定后,Proposer提出的编号更高的提案的value都是v呢?只要满足P2c即可:(约束P2c)对于任意的N和V,如果提案[N, V]被提出,那么存在一个半数以上的Acceptor组成的集合S,满足以下两个条件中的任意一个:
- S中每个Acceptor都没有接受过编号小于N的提案。
- S中Acceptor接受过的最大编号的提案的value为V。
为了满足P2b,这里有个比较重要的思想:Proposer生成提案之前,应该先去**『学习』已经被选定或者可能被选定的value,然后以该value作为自己提出的提案的value。如果没有value被选定,Proposer才可以自己决定value的值。这样才能达成一致。这个学习的阶段是通过一个『Prepare请求』实现的。于是我们得到了如下的提案生成算法**:
- Proposer选择一个新的提案编号N,然后向某个Acceptor集合(半数以上)发送请求,要求该集合中的每个Acceptor做出如下响应(response)。 (a) 向Proposer承诺保证不再接受任何编号小于N的提案。 (b) 如果Acceptor已经接受过提案,那么就向Proposer响应已经接受过的编号小于N的最大编号的提案。我们将该请求称为编号为N的Prepare请求。
- 如果Proposer收到了半数以上的Acceptor的响应,那么它就可以生成编号为N,Value为V的提案[N,V]。这里的V是所有的响应中编号最大的提案的Value。如果所有的响应中都没有提案,那 么此时V就可以由Proposer自己选择。 生成提案后,Proposer将该提案发送给半数以上的Acceptor集合,并期望这些Acceptor能接受该提案。我们称该请求为Accept请求。(注意:此时接受Accept请求的Acceptor集合不一定是之前响应Prepare请求的Acceptor集合)
Acceptor可以忽略任何请求(包括Prepare请求和Accept请求)而不用担心破坏算法的安全性。因此,我们这里要讨论的是什么时候Acceptor可以响应一个请求。我们对Acceptor接受提案给出如下约束:(约束P1a)一个Acceptor只要尚未响应过任何编号大于N的Prepare请求,那么他就可以接受这个编号为N的提案。
如果Acceptor收到一个编号为N的Prepare请求,在此之前它已经响应过编号大于N的Prepare请求。根据P1a,该Acceptor不可能接受编号为N的提案。因此,该Acceptor可以忽略编号为N的Prepare请求。当然,也可以回复一个error,让Proposer尽早知道自己的提案不会被接受。因此,一个Acceptor只需记住:1. 已接受的编号最大的提案 2. 已响应的请求的最大编号。
Paxos算法分为两个阶段。具体如下:
-
阶段一:
(a) Proposer选择一个提案编号N,然后向半数以上的Acceptor发送编号为N的Prepare请求。
(b) 如果一个Acceptor收到一个编号为N的Prepare请求,且N大于该Acceptor已经响应过的所有Prepare请求的编号,那么它就会将它已经接受过的编号最大的提案(如果有的话)作为响应反馈给Proposer,同时该Acceptor承诺不再接受任何编号小于N的提案。
-
阶段二:
(a) 如果Proposer收到半数以上Acceptor对其发出的编号为N的Prepare请求的响应,那么它就会发送一个针对**[N,V]提案的Accept请求给半数以上的Acceptor。注意:V就是收到的响应中编号最大的提案的value**,如果响应中不包含任何提案,那么V就由Proposer自己决定。
(b) 如果Acceptor收到一个针对编号为N的提案的Accept请求,只要该Acceptor没有对编号大于N的Prepare请求做出过响应,它就接受该提案。
Learner学习(获取)被选定的value有如下三种方案:
通过选取主Proposer,就可以保证Paxos算法的活性。至此,我们得到一个既能保证安全性,又能保证活性的分布式一致性算法——Paxos算法。
https://www.cnblogs.com/linbingdong/p/6253479.html
NWR是一种在分布式存储系统中用于控制一致性级别的一种策略。在亚马逊的云存储系统中,就应用 NWR来控制一致性。
N:在分布式存储系统中,有**多少份备份数据** 。
W:代表一次成功的更新操作要求至少**有w份数据写入成功** **。**
R: 代表一次成功的读数据操作要求至少**有R份数据成功读取。**
NWR值的不同组合会产生不同的一致性效果,当W+R>N的时候,整个系统对于客户端来讲能保证强一致性。
以常见的N=3、W=2、R=2为例: N=3,表示,任何一个对象都必须有三个副本 W=2表示,对数据的修改操作只需要在3个副本中的2个上面完成就返回 R=2表示,从三个对象中要读取到2个数据对象,才能返回
1.当W是2、R是2的时候,W+R>N,这种情况对于客户端就是强一致性的。
如果R+W>N,则读取操作和写入操作成功的数据一定会有交集(如图中的 Node2),这样就可以保证一定能够读取到最新版本的更新数据,数据的强一致性得到了保证。在满足数据一致性协议的前提下,R或者W设置的越大,则系统延迟越大,因为这取决于最慢的那份备份数据的响应时间。
2. 当R+W<=N,无法保证数据的强一致性
因为成功写和成功读集合可能不存在交集,这样读操作无法读取到最新的更新数值,也就无法保证数据的强一致性。
分布式存储系统通常通过维护多个副本来进行容错,提高系统的可用性。要实现此目标,就必须要解决分布式存储系统的最核心问题:维护多个副本的一致性。
首先需要解释一下什么是一致性(consensus),它是构建具有容错性(fault-tolerant)的分布式系统的基础。 在一个具有一致性的性质的集群里面,同一时刻所有的结点对存储在其中的某个值都有相同的结果,即对其共享的存储保持一致。集群具有自动恢复的性质,当少数结点失效的时候不影响集群的正常工作,当大多数集群中的结点失效的时候,集群则会停止服务(不会返回一个错误的结果)。
一致性协议就是用来干这事的,用来保证即使在部分(确切地说是小部分)副本宕机的情况下,系统仍然能正常对外提供服务。一致性协议通常基于replicated state machines,即所有结点都从同一个state出发,都经过同样的一些操作序列(log),最后到达同样的state。
系统中每个结点有三个组件:
状态机: 当我们说一致性的时候,实际就是在说要保证这个状态机的一致性。状态机会从log里面取出所有的命令,然后执行一遍,得到的结果就是我们对外提供的保证了一致性的数据
Log: 保存了所有修改记录
一致性模块: 一致性模块算法就是用来保证写入的log的命令的一致性,这也是raft算法核心内容
Raft协议将一致性协议的核心内容分拆成为几个关键阶段,以简化流程,提高协议的可理解性。Leader election(选主阶段)、Log Replication(日志复制阶段)、Safety(安全阶段)、Log Compaction
Raft协议的每个副本都会处于三种状态之一:Leader、Follower、Candidate。
Leader:所有请求的处理者,Leader副本接受client的更新请求,本地处理后再同步至多个其他副本;
Follower:请求的被动更新者,从Leader接受更新请求,然后写入本地日志文件
Candidate:如果Follower副本在一段时间内没有收到Leader副本的心跳,则判断Leader可能已经故障,此时启动选主过程,此时副本会变成Candidate状态,直到选主结束。
时间被分为很多连续的随机长度的term,term有唯一的id。每个term一开始就进行选主:
- Follower将自己维护的current_term_id加1。
- 然后将自己的状态转成Candidate
- 发送RequestVoteRPC消息(带上current_term_id) 给 其它所有server
这个过程会有三种结果:
- 自己被选成了主。当收到了majority的投票后,状态切成Leader,并且定期给其它的所有server发心跳消息(不带log的AppendEntriesRPC)以告诉对方自己是current_term_id所标识的term的leader。每个term最多只有一个leader,term id作为logical clock,在每个RPC消息中都会带上,用于检测过期的消息。当一个server收到的RPC消息中的rpc_term_id比本地的current_term_id更大时,就更新current_term_id为rpc_term_id,并且如果当前state为leader或者candidate时,将自己的状态切成follower。如果rpc_term_id比本地的current_term_id更小,则拒绝这个RPC消息。
- 别人成为了主。如1所述,当Candidator在等待投票的过程中,收到了大于或者等于本地的current_term_id的声明对方是leader的AppendEntriesRPC时,则将自己的state切成follower,并且更新本地的current_term_id。
- 没有选出主。当投票被瓜分,没有任何一个candidate收到了majority的vote时,没有leader被选出。这种情况下,每个candidate等待的投票的过程就超时了,接着candidates都会将本地的current_term_id再加1,发起RequestVoteRPC进行新一轮的leader election。
投票策略:
- 每个节点只会给每个term投一票,具体的是否同意和后续的Safety有关。
- 当投票被瓜分后,所有的candidate同时超时,然后有可能进入新一轮的票数被瓜分,为了避免这个问题,Raft采用一种很简单的方法:每个Candidate的election timeout从150ms-300ms之间随机取,那么第一个超时的Candidate就可以发起新一轮的leader election,带着最大的term_id给其它所有server发送RequestVoteRPC消息,从而自己成为leader,然后给他们发送心跳消息以告诉他们自己是主。
当Leader被选出来后,就可以接受客户端发来的请求了,每个请求包含一条需要被replicated state machines执行的命令。leader会把它作为一个log entry append到日志中,然后给其它的server发AppendEntriesRPC请求。当Leader确定一个log entry被safely replicated了(大多数副本已经将该命令写入日志当中),就apply这条log entry到状态机中然后返回结果给客户端。如果某个Follower宕机了或者运行的很慢,或者网络丢包了,则会一直给这个Follower发AppendEntriesRPC直到日志一致。当一条日志是commited时,Leader才可以将它应用到状态机中。Raft保证一条commited的log entry已经持久化了并且会被所有的节点执行。当一个新的Leader被选出来时,它的日志和其它的Follower的日志可能不一样,这个时候,就需要一个机制来保证日志的一致性。一个新leader产生时,集群状态可能如下:
最上面这个是新Leader,a~f是Follower,每个格子代表一条log entry,格子内的数字代表这个log entry是在哪个term上产生的。新Leader产生后,就以Leader上的log为准。其它的follower要么少了数据比如b,要么多了数据,比如d,要么既少了又多了数据,比如f。因此,需要有一种机制来让leader和follower对log达成一致,leader会为每个follower维护一个nextIndex,表示leader给各个follower发送的下一条log entry在log中的index,初始化为leader的最后一条log entry的下一个位置。leader给follower发送AppendEntriesRPC消息,带着(term_id, (nextIndex-1)), term_id即(nextIndex-1)这个槽位的log entry的term_id,follower接收到AppendEntriesRPC后,会从自己的log中找是不是存在这样的log entry,如果不存在,就给leader回复拒绝消息,然后leader则将nextIndex减1,再重复,知道AppendEntriesRPC消息被接收。
以leader和b为例: 初始化,nextIndex为11,leader给b发送AppendEntriesRPC(6,10),b在自己log的10号槽位中没有找到term_id为6的log entry。则给leader回应一个拒绝消息。接着,leader将nextIndex减一,变成10,然后给b发送AppendEntriesRPC(6, 9),b在自己log的9号槽位中同样没有找到term_id为6的log entry。循环下去,直到leader发送了AppendEntriesRPC(4,4),b在自己log的槽位4中找到了term_id为4的log entry。接收了消息。随后,leader就可以从槽位5开始给b推送日志了。
哪些follower有资格成为leader?
Raft保证被选为新leader的节点拥有所有已提交的log entry,这与ViewStamped Replication不同,后者不需要这个保证,而是通过其他机制从follower拉取自己没有的提交的日志记录
这个保证是在RequestVoteRPC阶段做的,candidate在发送RequestVoteRPC时,会带上自己的最后一条日志记录的term_id和index,其他节点收到消息时,如果发现自己的日志比RPC请求中携带的更新,拒绝投票。日志比较的原则是,如果本地的最后一条log entry的term id更大,则更新,如果term id一样大,则日志更多的更大(index更大)。
哪些日志记录被认为是commited?
1、leader正在replicate当前term(即term 2)的日志记录给其它Follower,一旦leader确认了这条log entry被majority写盘了,这条log entry就被认为是committed。如图a,S1作为当前term即term2的leader,log index为2的日志被majority写盘了,这条log entry被认为是commited 2、leader正在replicate更早的term的log entry给其它follower。图b的状态是这么出来的。
对协议的一点修正
在实际的协议中,需要进行一些微调,这是因为可能会出现下面这种情况:
- 在阶段a,term为2,S1是Leader,且S1写入日志(term, index)为(2, 2),并且日志被同步写入了S2;
- 在阶段b,S1离线,触发一次新的选主,此时S5被选为新的Leader,此时系统term为3,且写入了日志(term, index)为(3, 2);
- S5尚未将日志推送到Followers变离线了,进而触发了一次新的选主,而之前离线的S1经过重新上线后被选中变成Leader,此时系统term为4,此时S1会将自己的日志同步到Followers,按照上图就是将日志(2, 2)同步到了S3,而此时由于该日志已经被同步到了多数节点(S1, S2, S3),因此,此时日志(2,2)可以被commit了(即更新到状态机);
- 在阶段d,S1又很不幸地下线了,系统触发一次选主,而S5有可能被选为新的Leader(这是因为S5可以满足作为主的一切条件:1. term = 3 > 2, 2. 最新的日志index为2,比大多数节点(如S2/S3/S4的日志都新),然后S5会将自己的日志更新到Followers,于是S2、S3中已经被提交的日志(2,2)被截断了,这是致命性的错误,因为一致性协议中不允许出现已经应用到状态机中的日志被截断。
为了避免这种致命错误,需要对协议进行一个微调:只允许主节点提交包含当前term的日志
针对上述情况就是:即使日志(2,2)已经被大多数节点(S1、S2、S3)确认了,但是它不能被Commit,因为它是来自之前term(2)的日志,直到S1在当前term(4)产生的日志(4, 3)被大多数Follower确认,S1方可Commit(4,3)这条日志,当然,根据Raft定义,(4,3)之前的所有日志也会被Commit。此时即使S1再下线,重新选主时S5不可能成为Leader,因为它没有包含大多数节点已经拥有的日志(4,3)。
在实际的系统中,不能让日志无限增长,否则系统重启时需要花很长的时间进行回放,从而影响availability。Raft采用对整个系统进行snapshot来处理,snapshot之前的日志都可以丢弃。Snapshot技术在Chubby和ZooKeeper系统中都有采用。
Raft使用的方案是:每个副本独立的对自己的系统状态进行Snapshot,并且只能对已经提交的日志记录(已经应用到状态机)进行snapshot。
Snapshot中包含以下内容:
- 日志元数据,最后一条commited log entry的 (log index, last_included_term)。这两个值在Snapshot之后的第一条log entry的AppendEntriesRPC的consistency check的时候会被用上,之前讲过。一旦这个server做完了snapshot,就可以把这条记录的最后一条log index及其之前的所有的log entry都删掉。
- 系统状态机:存储系统当前状态(这是怎么生成的呢?)
snapshot的缺点就是不是增量的,即使内存中某个值没有变,下次做snapshot的时候同样会被dump到磁盘。当leader需要发给某个follower的log entry被丢弃了(因为leader做了snapshot),leader会将snapshot发给落后太多的follower。或者当新加进一台机器时,也会发送snapshot给它。发送snapshot使用新的RPC,InstalledSnapshot。
做snapshot有一些需要注意的性能点,1. 不要做太频繁,否则消耗磁盘带宽。 2. 不要做的太不频繁,否则一旦节点重启需要回放大量日志,影响可用性。系统推荐当日志达到某个固定的大小做一次snapshot。3. 做一次snapshot可能耗时过长,会影响正常log entry的replicate。这个可以通过使用copy-on-write的技术来避免snapshot过程影响正常log entry的replicate。
集群拓扑变化
集群拓扑变化的意思是在运行过程中多副本集群的结构性变化,如增加/减少副本数、节点替换等。
Raft协议定义时也考虑了这种情况,从而避免由于下线老集群上线新集群而引起的系统不可用。Raft也是利用上面的Log Entry和一致性协议来实现该功能。
假设在Raft中,老集群配置用Cold表示,新集群配置用Cnew表示,整个集群拓扑变化的流程如下:
- 当集群成员配置改变时,leader收到人工发出的重配置命令从Cold切成Cnew;
- Leader副本在本地生成一个新的log entry,其内容是Cold∪Cnew,代表当前时刻新旧拓扑配置共存,写入本地日志,同时将该log entry推送至其他Follower节点
- Follower副本收到log entry后更新本地日志,并且此时就以该配置作为自己了解的全局拓扑结构,
- 如果多数Follower确认了Cold U Cnew这条日志的时候,Leader就Commit这条log entry;
- 接下来Leader生成一条新的log entry,其内容是全新的配置Cnew,同样将该log entry写入本地日志,同时推送到Follower上;
- Follower收到新的配置日志Cnew后,将其写入日志,并且从此刻起,就以该新的配置作为系统拓扑,并且如果发现自己不在Cnew这个配置中会自动退出
- Leader收到多数Follower的确认消息以后,给客户端发起命令执行成功的消息
异常分析
- 如果Leader的Cold U Cnew尚未推送到Follower,Leader就挂了,此时选出的新的Leader并不包含这条日志,此时新的Leader依然使用Cold作为全局拓扑配置
- 如果Leader的Cold U Cnew推送到大部分的Follower后就挂了,此时选出的新的Leader可能是Cold也可能是Cnew中的某个Follower;
- 如果Leader在推送Cnew配置的过程中挂了,那么和2一样,新选出来的Leader可能是Cold也可能是Cnew中的某一个,那么此时客户端继续执行一次改变配置的命令即可
- 如果大多数的Follower确认了Cnew这个消息后,那么接下来即使Leader挂了,新选出来的Leader也肯定是位于Cnew这个配置中的,因为有Raft的协议保证。
为什么需要弄这样一个两阶段协议,而不能直接从Cold切换至Cnew?这是因为,如果直接这么简单粗暴的来做的话,可能会产生多主。简单说明下:
假设Cold为拓扑为(S1, S2, S3),且S1为当前的Leader,如下图:
假如此时变更了系统配置,将集群范围扩大为5个,新增了S4和S5两个服务节点,这个消息被分别推送至S2和S3,但是假如只有S3收到了消息并处理,S2尚未得到该消息
这时在S2的眼里,拓扑依然是<S1, S2, S3>,而在S3的眼里拓扑则变成了<S1, S2, S3, S4, S5>。假如此时由于某种原因触发了一次新的选主,S2和S3分别发起选主的请求:
最终,候选者S2获得了S1和S2自己的赞成票,那么在它眼里,它就变成了Leader,而S3获得了S4、S5和S3自己的赞成票,在它眼里S3也变成了Leader,那么多Leader的问题就产生了。而产生该问题的最根本原因是S2和S3的系统视图不一致。
它将整个算法的实现分为三个阶段,防止像Paxos算法那样将整个过程杂糅在一起,导致理解困难,主要分为选主阶段、日志复制阶段以及安全状态。 Strong leader:通过选举出主节点负责将Log复制到其他服务器,使得Raft算法简单易懂。 Leader election:每一个节点通过sleep一个随机的timeout,每一个server有一个id,然后 通过投票选举。 Membership changes:有时候,集群可能需要进行升级或者更改配置,它可以通过joint consensus的方式支持在线上更改配置,并且在这个阶段保证整个集群的可用性。 snapshot:每一台机器维持着一份副本,这样可以在机器宕机恢复的时候读取lastest commitId进行恢复。
传统的 Linux 操作系统的标准 I/O 接口是基于数据拷贝操作的,即 I/O 操作会导致数据在操作系统内核地址空间的缓冲区和应用程序地址空间定义的缓冲区之间进行传输。这样做最大的好处是可以减少磁盘 I/O 的操作,因为如果所请求的数据已经存放在操作系统的高速缓冲存储器中,那么就不需要再进行实际的物理磁盘 I/O 操作。但是数据传输过程中的数据拷贝操作却导致了极大的 CPU 开销,限制了操作系统有效进行数据传输操作的能力。
零拷贝( zero-copy )技术可以有效地改善数据传输的性能,在内核驱动程序(比如网络堆栈或者磁盘存储驱动程序)处理 I/O 数据的时候,零拷贝技术可以在某种程度上减少甚至完全避免不必要 CPU 数据拷贝操作。
零拷贝就是一种避免 CPU 将数据从一块存储拷贝到另外一块存储的技术。针对操作系统中的设备驱动程序、文件系统以及网络协议堆栈而出现的各种零拷贝技术极大地提升了特定应用程序的性能,并且使得这些应用程序可以更加有效地利用系统资源。这种性能的提升就是通过在数据拷贝进行的同时,允许 CPU 执行其他的任务来实现的。
零拷贝技术可以减少数据拷贝和共享总线操作的次数,消除传输数据在存储器之间不必要的中间拷贝次数,从而有效地提高数据传输效率。而且,零拷贝技术减少了用户应用程序地址空间和操作系统内核地址空间之间因为上下文切换而带来的开销。进行大量的数据拷贝操作其实是一件简单的任务,从操作系统的角度来说,如果 CPU 一直被占用着去执行这项简单的任务,那么这将会是很浪费资源的;如果有其他比较简单的系统部件可以代劳这件事情,从而使得 CPU 解脱出来可以做别的事情,那么系统资源的利用则会更加有效。综上所述,零拷贝技术的目标可以概括如下:
- 避免数据拷贝 ①避免操作系统内核缓冲区之间进行数据拷贝操作。 ②避免操作系统内核和用户应用程序地址空间这两者之间进行数据拷贝操作。 ③用户应用程序可以避开操作系统直接访问硬件存储。 ④数据传输尽量让 DMA 来做。
- 综合目标 ①避免不必要的系统调用和上下文切换。 ②需要拷贝的数据可以先被缓存起来。 ③对数据进行处理尽量让硬件来做。
参考:https://www.jianshu.com/p/580a14db9d77
当作业调度中采用该算法时,每次调度都是从后备作业队列中选择一个或者多个最先进入该队列的任务,将他们调入内存,为他们分配资源,创建进程,然后放进就绪队列,在进程调度中采用FCFS算法时,则每次是从就绪队列选择一个最先进入该队列的进程,为之分配处理机,使之投入运行,该进程一直运行到完成或者发生事件而阻塞后才放弃处理机,特点是,算法比较简单,可以实现基本的公平。
短作业优先调度算法是从后备队列中选择一个或者若干个估计运行时间最短的作业,将他们调入内存运行,而短进程优先调度算法,则是从就绪队列中选择一个估计运行时间最短的进程,将处理机分配给他,使他立即执行并一直执行到完成或发生某事件而被阻塞放弃处理机时在重新调度,该算法未照顾紧迫性作业。
- 为了照顾紧迫型任务,使之在进入系统后边获得优先处理,引入了最高优先权优先调度算法,当把该算法用于紧迫性作业调度时,系统将从后备队列中选择若干个优先级最高的作业装入内存中,当用于进程调度时,该算法是把处理机分配给就绪队列中优先权最高的进程。
①非抢占式优先权算法
在这种方式下,系统一旦把处理机分配给就绪队列中优先级最高的进程后,该进程便一致执行下去,直至完成或发生某些事件而发生阻塞使该进程放弃处理机时,这种调度算法主要用于批处理系统中。也可用于某些实时性要求不严的实时系统中。
②抢占式优先权调度算法
在这种方式下,系统同样是把处理机分配给优先权高的进程,使之执行,但是**在执行期间,只要出现了另一个优先级更高的进程,当前进程就会立即停止执行。重新将处理机分配给新的优先级更高的进程。**显然,这种抢占式优先权调度算法能够更好的满足紧迫性作业的需求,故而常用于要求比较严格的实时系统中,以及对性能要求较高的批处理和分时系统中。
- 高响应比优先调度算法
在批处理系统中,短作业优先算法是一种比较好的算法,其主要的不足是长作业的运行得不到保证,如果我们能够为每个作业引入动态优先级,并使作业的优先级随着等待时间的增加而以速率a提高,则长作业在等待一段时间后,必然有机会分配到处理机。该优先权的变化规律可描述为:Rp=(等待时间+要求服务时间)/要求服务时间=响应时间/要求服务时间
(1)如果作业等待时间相同,则要求服务时间越短,其优先级越高,因而该算法有利于短作业。
(2)当要求服务时间相同时,作业的优先权决定其等待时间,等待时间越长,其优先级越高,因而他实现的是先来先服务。
(3)对于长作业,作业的优先级可以随着等待时间的增加而升高,当其等待时间足够长时,其优先级便可提升到很高,从而获得处理机。简言之,该算法既照顾了短作业,又考虑了作业到达的先后顺序,不会使长作业长时间得不到服务。因此,该算法实现了一种比较好的折中。当然,在利用该算法时,每次进行调度算法前,都需先进行响应比计算,这样会增加系统的开销。
在早期的时间片轮转法中,系统将所有的就绪进程按照先来先服务的原则排成一个队列,每次调度时,并分配给队头进程,并令其执行一个时间片,时间片的大小在几毫秒到几百毫秒之间,当时间片用完时,有一个计时器发出时钟终端请求,调度程序变根据此信号来停止进程的执行。并将该进程放到队列的队尾。然后再把处理机分配给新的队头进程,同时让它执行一个时间片,这样就可以保证就绪队列中的每个进程在一个给定的时间片得以执行。
(1)应设置读个就绪队列,并为各个队列赋予不同的优先级,第一个队列的优先级最高,第二个队列次之,其余队列的优先级逐个降低,该算法赋予各个队列中进程执行时间片的大小也各不相同,在优先级越高的队列中,为每个进程所规定的执行时间片就越小。例如,第二个队列的时间片要比第一个队列的时间片长一倍.....,第i+1个队列要比第i个队列的时间片要长一倍。
(2)当一个新的进程进入到内存后,首先将他放到第一个队列的末尾,按照FCFS的原则排队等待调度,当轮到该进程执行时,入它能够在该时间片执行完成,则可直接撤离系统。如果没有在一个时间片内完成,调度程序便将他转入第二个队列的末尾,在按照同样的FCFS的原则等待调度执行。如果又运行了一个时间片还没有完成,则放入第三个队列。如此下去,当一个长作业进入第n级队列(优先级最低的队列)后,在第n级队列便采取按照时间片轮转的方式运行。
(3)仅当第一级队列空闲时,调度程序才调度第二级队列中的进程运行,仅当1~(i-1)队列均为空时,才会调度第i级队列中的进程运行。如果处理机正在第i级队列中为某进程服务时,又有新的进程进入优先级较高的队列(第1~(i-1)级队列中的任何队列中),则此时新进程将抢占正在运行进程的处理机,即由调度程序把正在运行的进程放回第i级队列末尾,把处理机分配给高优先权进程。
在多级反馈队列调度算法中,如果规定一个队列时间片略大于多数人机交互所需之处理时间,便能够较好的满足各种类型用户的需要。











































































